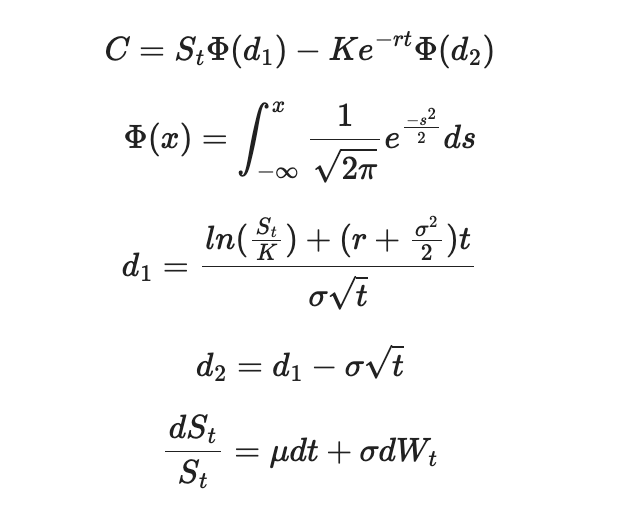
Fibonacci Ratios  

Leonardo Pisano was known for most of his life as Fibonacci. Fibonacci was inspired to write Liber Abaci on a visit to the Algerian City of Bugia, where an Arab mathematician revealed to him the wonders of the Hindu-Arabic numbering system that Arab mathematicians had introduced to the West during the Crusades. When Fibonacci saw all the calculations that this system made possible, calculations that could not possibly be managed with Roman letter numerals, he set about learning everything he could about it. The Fibonacci Ratio embodies a beautiful collaboration of Western and Eastern calculations that led to something of a mathematical miracle.

Divide any of the Fibonacci numbers by the next higher number. After 3, the answer is always 0.625. After 89, the answer is always 0.618; after higher numbers, more decimal places can be filled in. Divide any number by its preceding number. After 2, the answer is always 1.6. After 144, the answer is always 1.618.

The Greeks knew this proportion and called it "the golden mean." The golden mean also appears throughout nature-in flower patterns, the leaves of an artichoke, and the leaf stubs on a palm tree. It is also the ratio of the length of the human body above the navel to its length below the navel (in normally proportioned people, that is). The length of each successive bone in our fingers, from tip to hand, also bears this ratio. In one of its more romantic manifestations, the Fibonacci ratio defines the proportions and shape of a beautiful spiral that appears in the shape of certain galaxies, in a ram's horn, in many seashells, and in the coil of the ocean waves that surfers ride. The structure maintains its form without change as it is made larger and larger and regardless of the size of the initial square with which the process is launched: form is independent of growth.

The journalist William Hoffer has remarked, "The great golden spiral seems to be nature's way of building quantity without sacrificing quality." The Fibonacci numbers can be used to make a wide variety of predictions, especially predictions about the stock market. Since 1962, Fibonacci's Liber Abaci was a spectacular first step in making measurement the key factor in the taming of risk.

Bernstein, Peter L. Against the Gods : The Remarkable Story of Risk. New York, John Wiley & Sons, 1996.

Luxsolis Investments uses Fibonacci ratios to identify patterns. Fibonacci retracements are horizontal levels drawn on a chart to indicate possible support or resistance zones where price might reverse during a pullback. Fibonacci extensions are levels beyond 100% that help traders estimate where price might go after a breakout or trend continuation.

Retracements

• 0.236 (23.6%)
• 0.382 (38.2%)
• 0.500 (50%)
• 0.618 (61.8%) ← the “Golden Ratio”
• 0.786 (78.6%)

Extensions

• 1.272 (127.2%)
• 1.618 (161.8%)
• 2.000 (200%)
• 2.618 (261.8%)

Fibonacci ratios are useful for setting up entry and exit points. By using these levels, quant trading is simple, allowing a trader to lock in profits by sticking to a numerical framework that removes the element of fear and greed from the equation.